1.物种多样性
物种多样性(species diversity)指群落是那些动植物组成的、组成群落的物种名录及各物种种群大小或数量,是生物群落的基本特征之一,是衡量群落多样性的基础。物种多样性包括种丰富性(species
richness)和群落异质性(hetrerogeneity)。种丰富性是指群落中物种数目的大小,群落异质性指群落中各个种的相对密度[与均匀性(species
evenness)呈正比],它决定着群落的功能特点。也就是说群落物种多样性反映了两层含义,一是群落中的物种数(number);二是各个物种所拥有的个体数目及其分布特点。一个群落中,物种的数目越多,且各个物种之间的个体数分布越均匀,那么这个群落的多样性就越大。
物种多样性测定(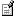 1)(
1)(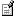 2)(
2)(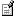 3)(
3)(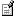 4)
4)
物种多样性可用多样性指数(diversity index)而数量化,多样性指数是反映种丰富性和异质性的综合指标,它是根据生物组成结构中种的数目和各个种的个体数目的分配特点而设计的一种数值指标,其主要目的是要将生态系或群落结构方面的这一特征与其它的一些特征如生产力、稳定性、环境类型等联系起来,并利用这一特性的变化来判断外来干扰(如污染)的影响。
(1)丰富度指数(richness indices)�
(1)Gleason(1922)指数:表明一定面积的生境内生物种类的数目。
dGl = (S-1)/lnA
式中A为单位面积,S为群落中的物种数目。
(2)Margalef指数(Margalef’s index)
dM = (S-1)/ ln N
式中S为总种数,N为群落总个体数。(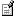 首部)
首部)
(2)辛普森多样性指数
辛普森多样性指数(Simpson’s diversity index)
表示从无限大的群落中随机抽取两个个体为同一种的概率。
D = 1- Σ(ni/N)2
式中nI为I种的个体数,N为群落的总个体数,S为总种数。(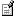 首部)
首部)
(3) 香农—威纳指数(Shannon- Wiener diversity index)
Shannnon多样性指数是群落中物种种类数和均匀性(各物种的个体相对比例)的函数。其计算公式如下:
s
Η′= -∑ Pilog2Pi
1
式中,Pi是第i种的个体数与该群落观察到的总个体数之比值;S是总种数种数;Η′为多样性指数,其值变动于零至任何正数之间。群落中当全部个体属于一个物种时,Η′=
0;全部个体各属于不同种时,Η′值最大。(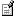 首部)
首部)
(4) 均匀性指数
多样性的概念包含着两个成分:一是群落中的物种数,有一个与种类数量增多相一致的多样性增加;二是各物种之间个体分布的均匀性。从生物学角度看,Η′的数值受个体数较多物种的影响较大,忽视了个体数稀少物种的作用。如果多样性指数仅以Η′来表示,我们无法确定多样性值变化的原因是由于群落中种类的增加所造成的还是由于每一物种个体的分布更均匀。因此,Pielou(1966)提出了均匀度J的概念,即实际多样性与理论上最大的多样性的比值。所谓理论上最大多样性就是假定群落中每一个体都属于不同的物种,这时多样性指数最大。即
Η′max = -S{1/S log2(1/S)}=log2(S)
则
J =Η′/Η′max
均匀度的大小衡量了群落中各个种个体数的差异程度,各个种个体数完全相同的集合,其均匀度J =1。(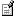 首部)
首部)
利科软件